자료구조/문제풀이
[백준 JAVA] 22948 원 이동하기 2
휴먼코딩
2024. 10. 2. 09:54
22948 원 이동하기 2
https://www.acmicpc.net/problem/22948
문제설명
평면에 N개의 원이 주어지고, 각 원은 x축 위에 위치한다.
- 어떤 두 원이 서로 만나지 않으며, 하나의 원이 다른 원의 내부에 포함될 수 있다.
- 한 원의 내부에서 다른 원의 내부로 이동할 때, 각 원의 내부는 한 번만 방문할 수 있다.
- 즉, 한 번 들어간 원의 내부는 다시 방문할 수 없다.
이동의 올바름
- 원 A의 내부에서 시작하여, 원 B의 내부로 직접 이동할 수 있는 경로를 찾는다.
- 경로를 따라 이동할 때, 만약 원의 내부를 거친다면 그 내부는 한 번만 방문해야 한다.
가능한 경우
- 원 A와 B가 서로 포함관계가 아니고 만나지 않는 경우:

원 A 내부 → 좌표평면 → 원 B 내부로 이동 가능 - 원 B가 원 A의 내부에 있는 경우:
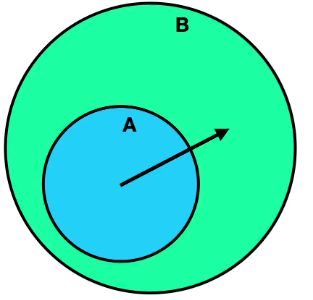
3. 원 A가 원 B의 내부에 있는 경우:

올바르지 않은 경우
- 여러 개의 원이 존재하며 포함관계가 아닌 경우:
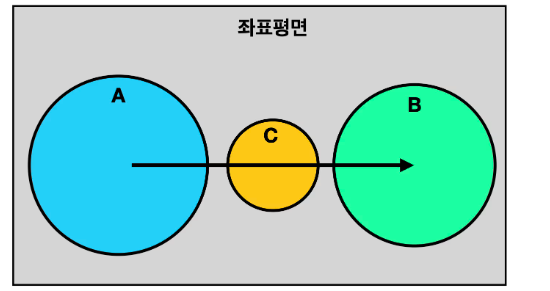
2. 원 B가 원 A의 내부에 있을 때:

문제풀이
- 그래프 구성:
- 각 노드의 좌표와 반경을 바탕으로 우선순위 큐를 사용하여 각 노드의 위치를 정렬하고
- 반경 내에 있는 노드들을 서로 연결한다.
- 인접 리스트를 구성한다.
- BFS (너비 우선 탐색):
- 시작 노드로부터 BFS를 수행하여 도착 노드까지의 경로를 찾는다.
- 방문한 노드를 체크하기 위해 배열을 사용하고, 현재 노드, 단계 수, 경로를 저장한다.
- BFS 도중 도착 노드에 도달하면 단계 수와 경로를 출력한다.
O(N log N) 시간복잡도
- 우선순위 큐를 통한 그래프 구성:
- 노드를 추가하는 데 O(logN)의 시간이 소요되며
- 총 N개의 노드가 있으므로 이 부분의 시간 복잡도는 O(NlogN)이.
- BFS 탐색:
- BFS는 각 노드를 한 번씩 방문하므로 O(N)O의 시간 복잡도를 가진다.
- 이때 각 노드의 인접 리스트를 통해 이웃 노드를 탐색하는 데 걸리는 시간도 포함된다.
- O(NlogN)+O(N)=O(NlogN)
전체코드
import java.util.*;
import java.io.*;
import java.awt.*;
public class Main {
// 그래프의 인접 리스트를 저장하기 위한 ArrayList
static ArrayList<Integer>[] nodeList;
// BFS에서 사용될 노드 클래스
static class node {
int node; // 현재 노드
int cnt; // 이 노드에 도달하기 위해 걸린 단계 수
String allNode; // 이 노드에 도달하기 위해 거친 경로
// 노드 생성자
public node(int node, int cnt, String allNode) {
this.node = node;
this.cnt = cnt;
this.allNode = allNode;
}
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 노드의 수
int N = Integer.parseInt(st.nextToken());
nodeList = new ArrayList[N + 1]; // 인접 리스트 초기화
for (int i = 0; i <= N; i++) nodeList[i] = new ArrayList<>();
// 포인트를 x좌표 기준으로 관리하기 위한 우선순위 큐
PriorityQueue<Point> pq = new PriorityQueue<>((o1, o2) -> {
return o1.x - o2.x; // 포인트를 x좌표 기준으로 비교
});
// 극단적인 포인트 추가
pq.add(new Point(-10000000, 0));
pq.add(new Point(10000000, 0));
// 각 노드의 속성을 읽고 포인트를 우선순위 큐에 추가
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
int k = Integer.parseInt(st.nextToken()); // 노드 ID
int x = Integer.parseInt(st.nextToken()); // X좌표
int r = Integer.parseInt(st.nextToken()); // 반경
// 각 노드의 범위를 나타내는 포인트 추가
pq.add(new Point(x - r, k)); // 범위의 왼쪽 끝
pq.add(new Point(x + r, k)); // 범위의 오른쪽 끝
}
// 포인트의 관계에 따라 트리(그래프)를 구축
makeTree(pq, -1);
// 경로 검색을 위한 시작 노드와 종료 노드 읽기
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
// BFS 초기화
boolean[] visit = new boolean[N + 1]; // 방문한 노드를 추적하기 위한 배열
Queue<node> que = new LinkedList<>();
visit[from] = true; // 시작 노드를 방문한 것으로 표시
que.add(new node(from, 1, "" + from)); // BFS를 시작하는 노드 추가
// BFS 루프
while (!que.isEmpty()) {
node now = que.poll(); // 현재 노드 가져오기
// 목적지에 도달했는지 확인
if (now.node == to) {
System.out.println(now.cnt); // 단계 수 출력
System.out.println(now.allNode); // 경로 출력
return; // 프로그램 종료
}
// 이웃 노드 탐색
for (int next : nodeList[now.node]) {
if (visit[next]) // 이미 방문한 노드는 건너뜀
continue;
visit[next] = true; // 노드를 방문한 것으로 표시
// 다음 노드를 큐에 추가
que.add(new node(next, now.cnt + 1, now.allNode + " " + next));
}
}
}
// 우선순위 큐로부터 트리 구조를 구축하는 재귀 메서드
static void makeTree(PriorityQueue<Point> pq, int parents) {
Point now = pq.poll(); // 현재 포인트 가져오기
// 부모가 있을 경우 현재 포인트와 부모 간의 연결 생성
if (parents != -1) {
nodeList[parents].add(now.y);
nodeList[now.y].add(parents);
}
// 다음 포인트가 같은 y값을 가질 때까지 트리 구축 계속
while (now.y != pq.peek().y) {
makeTree(pq, now.y);
}
pq.poll(); // 현재 처리된 포인트 제거
}
}