힙(Heap)은 특별한 구조의 완전 이진 트리(Complete Binary Tree)로, 주로 우선순위 큐(Priority Queue)를 구현하는 데 사용된다. 힙은 데이터의 삽입, 삭제, 조회 등의 작업을 처리하며 힙에는최소 힙(Min-Heap)과 최대 힙(Max-Heap) 두 가지 타입이 있다.
- 최소 힙(Min-Heap): 모든 부모 노드는 자식 노드보다 작거나 같다. 루트 노드가 가장 작은 값을 가진다.
- 최대 힙(Max-Heap): 모든 부모 노드는 자식 노드보다 크거나 같다. 루트 노드가 가장 큰 값을 가잔다.
힙의 기본 개념
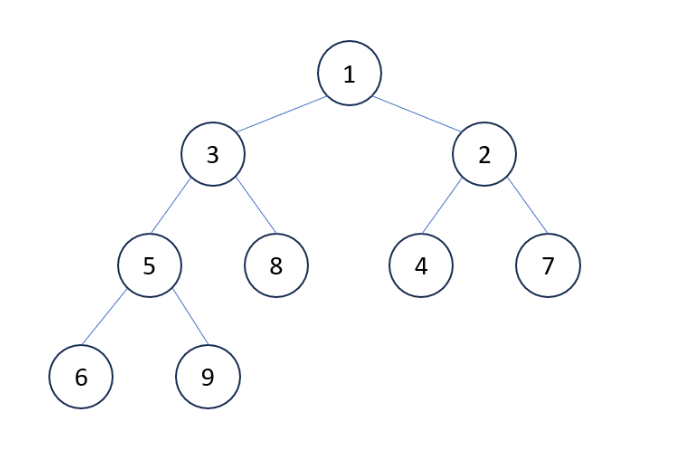
- 힙은 완전 이진 트리의 형태를 가지며, 모든 레벨이 완전히 채워져야 하고, 마지막 레벨은 왼쪽부터 채워져야 한다. 완전 이진 트리는 노드가 가능한 한 왼쪽에 밀집해 있는 트리이다.
힙의 주요 연산
- 삽입(Insert):
- 새 노드를 힙에 추가할 때, 먼저 트리의 마지막 레벨의 가장 왼쪽에 추가한다.
- 추가 후에는 힙의 성질을 유지하기 위해 노드를 부모 노드와 비교하여 필요시 교환하는 작업(업힙, heapify-up)을 수행한다.
- 삭제(Delete):
- 힙에서 가장 중요한 연산은 루트 노드의 삭제이다. 루트 노드는 최소 힙에서는 가장 작은 값, 최대 힙에서는 가장 큰 값을 가지고 있다.
- 루트 노드를 삭제하면, 트리의 마지막 레벨에서 가장 오른쪽의 노드를 루트로 이동시킨다.
- 그 다음, 힙의 성질을 유지하기 위해 "힙 속성 위반"을 해결하기 위해 노드를 자식 노드와 비교하여 필요시 교환하는 작업(다운힙, heapify-down)을 수행한다.
- 힙 속성 유지:
- 힙은 삽입이나 삭제 연산 후에도 그 특성(최소 힙 또는 최대 힙)을 유지한다. 이를 위해 heapify 연산을 사용한다.
힙의 시간 복잡도
- 삽입: O(log N) - 트리의 높이에 비례한다.
- 삭제(루트 삭제): O(log N) - 트리의 높이에 비례한다.
- 최소/최대값 조회: O(1) - 루트 노드를 조회한다.
힙의 구현
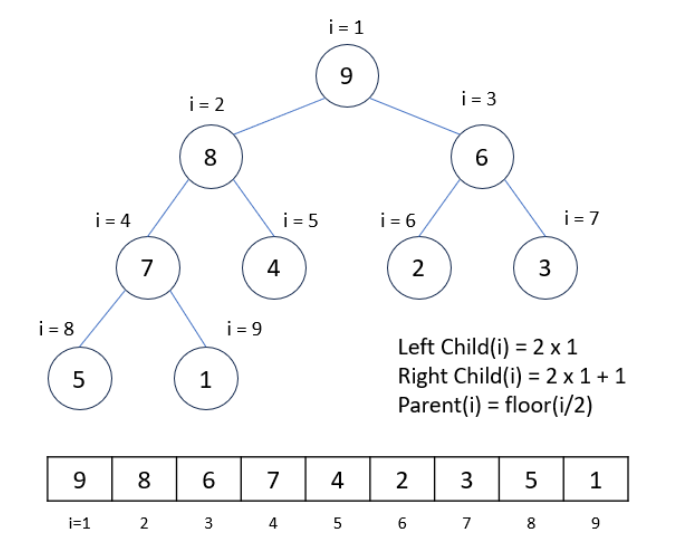
힙은 배열을 사용하여 구현할 수 있다. 배열에서 힙의 각 노드는 다음과 같은 인덱스 규칙을 가진다:
- 부모 노드의 인덱스가 i일 때:
- 왼쪽 자식 노드의 인덱스는 2 * i + 1
- 오른쪽 자식 노드의 인덱스는 2 * i + 2
- 자식 노드의 인덱스가 i일 때:
- 부모 노드의 인덱스는 (i - 1) / 2 (정수 나눗셈)
다익스트라 알고리즘(Dijkstra's Algorithm)
다익스트라 알고리즘은 그래프에서 특정 시작 노드에서 다른 모든 노드까지의 최단 경로를 찾기 위한 알고리즘이다. 이 알고리즘은 모든 엣지가 0 이상일때 적용되며 노드와 엣지로 구성된 그래프에서 출발 노드부터 각 노드까지의 최단 거리를 계산할 때 사용된다.
- 비음수 가중치: 다익스트라 알고리즘은 모든 엣지가 0 이상인 양수일때만 동작한다.
- 그리디 알고리즘: 다익스트라 알고리즘은 매 단계마다 현재까지 발견된 최단 거리를 기반으로 탐색을 진행하므로, 그리디 방식으로 최적의 해를 찾는다.
알고리즘의 작동 원리
- 초기화:
- 거리 배열(dist): 출발 노드에서 각 노드까지의 최단 거리를 저장하는 배열이다. 초기에는 출발 노드의 거리를 0으로 설정하고, 나머지 노드의 거리는 무한대(INF)로 설정한다.
- 우선순위 큐(Priority Queue): 현재까지 발견된 최단 거리 정보를 기반으로 노드를 처리하는 데 사용된다. 일반적으로 최소 힙을 사용하여 구현하며 큐에 출발 노드를 추가하고, 거리를 0으로 설정한다.
- 반복 과정:
- 노드 추출: 우선순위 큐에서 거리 값이 가장 작은 노드를 추출한다. 이 노드가 현재까지 발견된 최단 거리 정보를 가진 노드이다.
- 거리 업데이트: 현재 노드와 인접한 노드들에 대해 최단 거리를 업데이트한다. 현재 노드를 통해 각 인접 노드까지 가는 거리를 계산하고, 기존 거리보다 짧으면 거리를 갱신한다. 거리 업데이트 후, 변경된 노드를 우선순위 큐에 다시 추가한다.
- 우선순위 큐가 비어있을 때까지 위의 과정을 반복한다. 이 때, dist 배열에는 출발 노드에서 각 노드까지의 최단 거리가 저장된다.
알고리즘의 시간 복잡도
- 우선순위 큐를 배열로 구현: O(N^2) (노드의 수가 N일 때)
- 우선순위 큐를 이진 힙으로 구현: O((N + E) log N) (E는 엣지의 수)
이진 힙을 사용하여 구현할때 제곱근이 사용되는 배열보다 시간복잡도가 단축된다.
힙 메서드 구현 (자바)
import java.util.Arrays;
public class MinHeap {
private int[] heap;
private int size;
private static final int DEFAULT_CAPACITY = 10;
public MinHeap() {
heap = new int[DEFAULT_CAPACITY];
size = 0;
}
public void insert(int value) {
if (size == heap.length) {
ensureCapacity();
}
heap[size] = value;
size++;
heapifyUp(size - 1);
}
public int delete() {
if (size == 0) {
throw new IllegalStateException("Heap is empty");
}
int root = heap[0];
heap[0] = heap[size - 1];
size--;
heapifyDown(0);
return root;
}
public int getMin() {
if (size == 0) {
throw new IllegalStateException("Heap is empty");
}
return heap[0];
}
public void heapify(int[] array) {
heap = array;
size = array.length;
for (int i = (size / 2) - 1; i >= 0; i--) {
heapifyDown(i);
}
}
private void heapifyUp(int index) {
int parent = (index - 1) / 2;
if (index > 0 && heap[index] < heap[parent]) {
swap(index, parent);
heapifyUp(parent);
}
}
private void heapifyDown(int index) {
int leftChild = 2 * index + 1;
int rightChild = 2 * index + 2;
int smallest = index;
if (leftChild < size && heap[leftChild] < heap[smallest]) {
smallest = leftChild;
}
if (rightChild < size && heap[rightChild] < heap[smallest]) {
smallest = rightChild;
}
if (smallest != index) {
swap(index, smallest);
heapifyDown(smallest);
}
}
private void swap(int i, int j) {
int temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
private void ensureCapacity() {
heap = Arrays.copyOf(heap, heap.length * 2);
}
}연산별 시간 복잡도 비교
연산/자료구조스택(Stack)큐(Queue)우선순위 큐(Priority Queue)
| 삽입 | O(1) | O(1) | O(log N) |
| 삭제 | O(1) | O(1) | O(log N) |
| 최댓값/최솟값 얻기 | O(1) | O(1) | O(1) |
스택 (Stack):
- 삽입: 스택의 맨 위에 원소를 추가하는 연산. 상수 시간 O(1) 소요
- 삭제: 스택의 맨 위에 있는 원소를 제거하는 연산. 상수 시간 O(1) 소요
- 최댓값/최솟값 얻기: 스택의 맨 위에 있는 원소를 조회하는 연산. 상수 시간 O(1) 소요
- 큐 (Queue):
- 삽입: 큐의 뒤쪽에 원소를 추가하는 연산. 상수 시간 O(1) 소요
- 삭제: 큐의 앞쪽에서 원소를 제거하는 연산. 상수 시간 O(1) 소요
- 최댓값/최솟값 얻기: 큐의 앞쪽에 있는 원소를 조회하는 연산. 상수 시간 O(1) 소요
- 우선순위 큐 (Priority Queue):
- 삽입: 힙에 원소를 추가하는 연산. 로그 시간 O(log N) 소요
- 삭제: 힙에서 루트 노드를 삭제하는 연산. 로그 시간 O(log N) 소요
- 최댓값/최솟값 얻기: 힙의 루트 노드를 조회하는 연산. 상수 시간 O(1) 소요
